Data 311: Machine Learning

Lecture 16: Ridge Regression and LASSO

Dr. Irene Vrbik

University of British Columbia Okanagan

Recall: Linear Model

Recall the linear model:

\[ Y = \beta_0 + \beta_1 X_1 + ··· + \beta_p X_p + \epsilon \]

In ordinary least squares regression, estimates of the regression coefficients (i.e. the \(\beta\)s) are found by minimizing the residuals sum of squares (RSS) (this as our “cost” function)

\[RSS = \sum_{i=1}^n (y_i - \hat y_i)^2\]

• OLS may not be the best model
• we discuss some ways in which the simple linear model can be improved improved by replacing ordinary least squares fitting with some alternative fitting procedures.

Recap

• We’ve now seen a couple of alternatives to the linear model for regression.

• BUT, the linear model still reigns supreme in most realms of science due to its simplicity (which helps for inference).

• We can improve upon the linear model (both in terms of prediction accuracy and model interpretibility) by replacing ordinary least squares fitting with some alternative fitting procedures: shrinkage (aka regularization) methods.

• The are simple, easy to interpret and work well
• one of these models will perform feature selection for us (which is important when we risk overfitting and makes it easier to interpret and more useful)

Motivation

Prediction Accuracy

• It’s becoming more and more common that \(p > n\)
• In those scenarios there is no longer a unique least squares coefficient estimate and the model has higher variance.

• when \(p >n\) estimates of coefficients become unstable and can vary significantly with minor changes in the data.
• high variance –> unreliable predictions
• one solution to the \(p>n\) problem is to reduce the number of features.
• while this can improve in terms of prediction accuracy it also has the benefit of improving …

Model Interpretability

• By removing irrelevant predictors — or setting the corresponding coefficient estimates to zero — we can obtain a model that is more easily interpreted.

• Inference and interpretability – what are the factors that are driving the response

Non-unique solutions

Think about fitting a OLS line to a single observation.

Non-unique solutions

Think about fitting a OLS line to a single observation.

• This line has a 0 SSR

Non-unique solutions

Think about fitting a OLS line to a single observation.

• This line has a 0 SSR
• As does this one

Non-unique solutions

Think about fitting a OLS line to a single observation.

• This line has a 0 SSR
• As does this one
• As does this one

High Variance

Think about fitting a OLS line to two data points

• This line has a 0 SSR
• It has high variance
• And low bias

• You can imagine that this type model wouldn’t generalize well to new data points
• this line has high variance (two other random points from my training set would lead to very different line)
• we know that this model where the number of parameters \(\beta_0\), and \(\beta_1\) = number of observations is overfitting

Bias-Variance Tradeoff

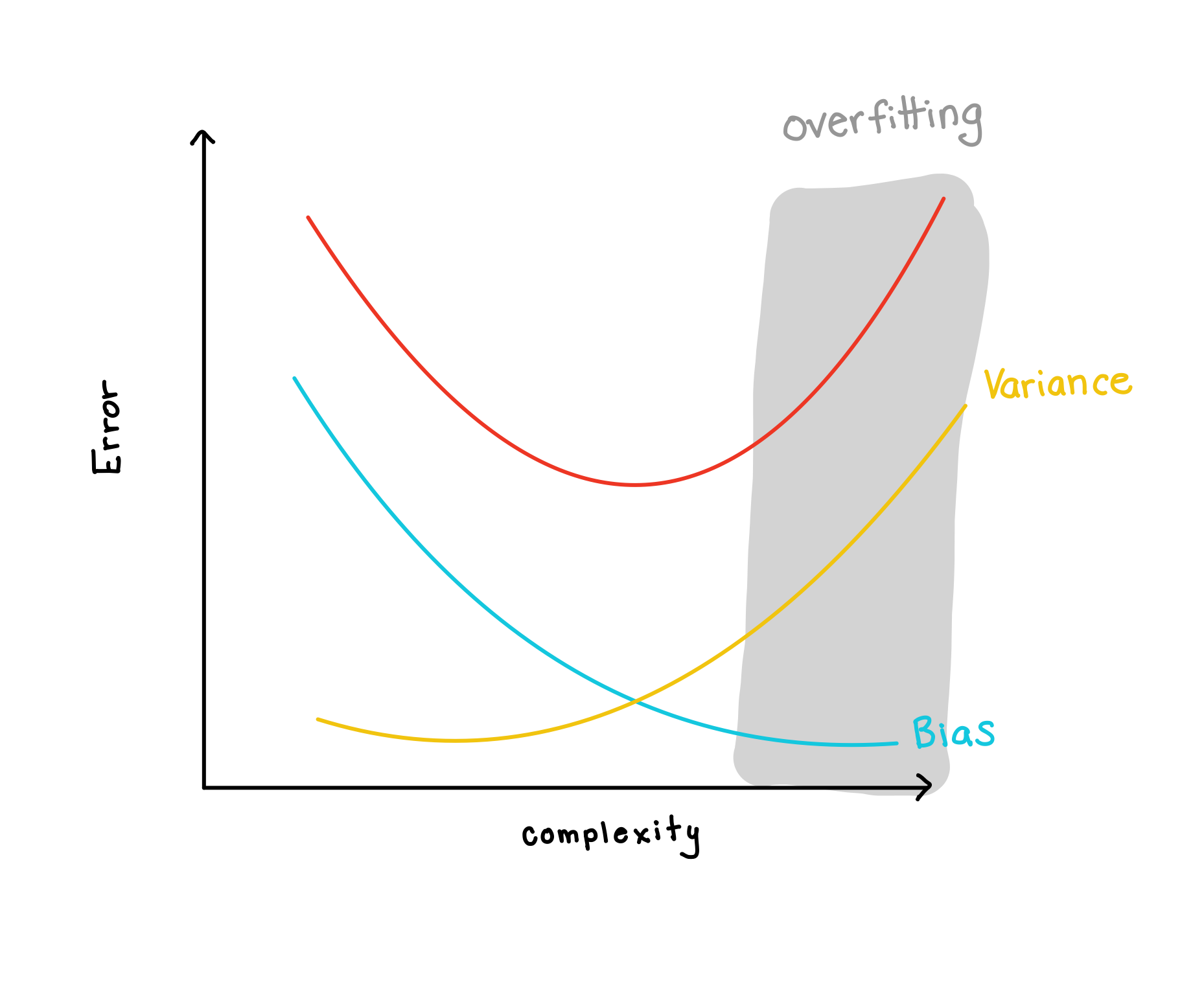
If n, the number of training observations, is much larger than p, the number of predictors, there can be a lot of variability in the least squares fit, resulting in overfitting and consequently poor predictions on future observations not used in model training.

• more generally, when \(p > n\) estimates may have high variance
• this leads to unreliable predictions
• why? see plot

Combatting High Variance

Instead of least squares, we will consider an alternative fitting procedure that will introduce a small amount of bias to get back a significant drop in variance (thereby improving prediction accuracy).

read caption

Variable Selection

• To combat this, we could use subset selection¹ wherein only a subset of the \(p\) predictors that we believe to be related to the response are used to fit the model (see Ch 6.1 in ISLR)

• Using cross-validated prediction error, for example, we could select a single best model from all possible models.

• For large \(p\), however, an exhaustive search of every possible subset of predictors is not computationally feasible²; furthermore it will be liable to overfit to the data.

• subset selection requires fitting \(2^p\) models (\(p\) = 10 means 1024 models, \(p = 40\) 1,099,512,000,000 over 1 trillion models).

• So we can pick the best model with \(k\) predictors by choosing the one that has the smallest test error

• authors suggest to only use this if you have a handful or two of predictors

• ridge regression and the lasso can be interpreted as computationally feasible alternatives to best subset selection

1. e.g. forward, backward, and mixed-stepwise selection

2. there are \({p \choose k}\) possible ways of choosing \(k\) predictors from \(p\) predictors

Ridge Regression

Ridge regression (RR) includes a penalty in the estimation process and aims to minimize:

\[\begin{gather} RSS + \lambda \sum_{j=1}^p \beta_j^2 = \sum_{i=1}^n ( y_i - \hat y_i)^2 + \lambda \sum_{j=1}^p \beta_j^2\\ = \sum_{i=1}^n (y_i - \beta_0 - \sum_{j=1}^p \beta_j x_{ij})^2+ \lambda \sum_{j=1}^p \beta_j^2 \end{gather}\] where \(\lambda \geq 0\) is a tuning parameter that shrinks the \(\beta_j\) estimates towards 0.

• this is going to penalize coefficients that are too large
• we pay a price for non-zero coefficents
• that price gets bigger as \(\beta_j\) gets bigger
• notice how \(\beta_0\) is omitted since it wouldn’t make sense to penalize that magnitude

Shrinkage penalty

• \(\lambda \sum_{j=1}^p \beta_j^2\) is the shrinkage penalty that will penalize the model for the total “size” of the coefficients¹

• The penalty will be small when \(\beta_1, \dots \beta_p\) are close to zero

• As \(\lambda\) increases the coefficient estimates will tend to “shrink” towards 0.

• Hence minimizing \(RSS + \lambda \sum_{j=1}^p \beta_j^2\) will encourage smaller (in magnitude) values for \(\beta_j\)

• λ controls the relative impact of this penalty on RSS
• Not unlike the cross complexity tuning we did for trees (where the penalty was \(\alpha\) times the size of the tree (terminal nodes))
• now instead of the number of the terminal nodes paying a cost, is the magnitude of the coefficients

1. the shrinkage penalty is not applied to the intercept \(\beta_0\)

Example: Credit

The Credit dataset contains information about credit card card holders and includes 11 variables including:

• Balance the average credit card debt for each individual (response) and several quantitative predictors:

  • Age, Cards (number of credit cards), Education (years of education), Income (in thousands of dollars), Limit (credit limit), and Rating (credit rating).

Fitting a least squares regression model to this data, we get…

MLR Credit fit

library(ISLR2); data(Credit)
lfit <- lm(Balance~., data = Credit)
(sfit <- summary(lfit))

...
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -479.20787   35.77394 -13.395  < 2e-16 ***
Income        -7.80310    0.23423 -33.314  < 2e-16 ***
Limit          0.19091    0.03278   5.824 1.21e-08 ***
Rating         1.13653    0.49089   2.315   0.0211 *  
Cards         17.72448    4.34103   4.083 5.40e-05 ***
Age           -0.61391    0.29399  -2.088   0.0374 *  
Education     -1.09886    1.59795  -0.688   0.4921    
OwnYes       -10.65325    9.91400  -1.075   0.2832    
StudentYes   425.74736   16.72258  25.459  < 2e-16 ***
MarriedYes    -8.53390   10.36287  -0.824   0.4107    
RegionSouth   10.10703   12.20992   0.828   0.4083    
RegionWest    16.80418   14.11906   1.190   0.2347    
---
...

With an Adjusted \(R^2\) of 0.9538.

Ridge Regression Coefficients

Unlike least squares, ridge regression will produce a different set of coefficient estimates, \(\beta^R_\lambda\), for each value of \(\lambda\)

ISLR Fig 6.4: The standardized ridge regression coefficients are displayed for the Credit data set, as a function of \(\lambda\) and standardized \(\ell_2\) norm.

• 1e-02 = 0.01, 1e+00 = 1, 1e+02 = 100
• when λ = 0, in which case the ridge regression coefficient estimate is the same as the least squares estimate, and so their ℓ2 norms are the same so \(|| \hat \beta^R ||_2/ || \hat \beta ||_2\) = 1
• right-hand panel can be thought of as the amount that the ridge regression coefficient estimates have been shrunken towards zero; a small value indicates that they have been shrunken very close to zero.
• standardized coefficients (cuz we scaled)

A note about norms

Another way we could have presented the penalty is through the norms. The p-norm (or \(\ell_p\) norm) is defined as:

\[ || x ||_p = \left(\sum_i |x_i|^p\right)^{1/p} \]

The 2-norm is Euclidean distance, \(|| x ||_2 = \sqrt{\left(\sum_i x_i^2\right)} = \sqrt{x_1^2 + x_2^2 + \ldots + x_i^2}\), and the Manhattan distance is the 1-norm (aka L1 norm): \(|| x ||_1 = \sum_i |x_i| = |x_1| + |x_2| + \ldots + |x_i|\)

where \(x\) is a of vector \(\mathbf {x} =(x_{1},\ldots ,x_{n})\)

L2 Regularization

The squared L2 norm in used in the Ridge Regression penalty:

\[ \lambda || \beta ||_2^2 = \lambda \sqrt{ \beta_1^2 + \beta_2^2 + \ldots + \beta_p^2 }^2 = \lambda\sum_{i=1}^p \beta_i^2 \]

• This process of adding a norm to our cost function is known as regularization.

• Hence this Ridge Regression is also known as L2 regularization.

• where \(\hat \beta\) denotes the vector of least squares coefficient estimates
• $|| ||_2 $ measures the distance of \(\hat \beta\) from zero

Tuning Parameter

• Clearly our choice for \(\lambda\) will be an important one (can you guess how we will find it?)

• If \(\lambda=0\) then the estimation process is simply least squares.

• As \(\lambda\) increases, the flexibility of the ridge regression fit decreases, leading to decreased variance but increased bias.

• As \(\lambda \rightarrow \infty\) then the penalty grows and the coefficients approach (but never equal) 0; this corresponds to the null model that contains no predictors.

• Clearly, some care is required in determining \(\lambda\).
• lambda encourages parametesr to be “shrunk” towards 0.
• how pushy it is will depend on the size of lambda
• recall if \(\beta_j\) is 0 then \(X_j\) doesn’t appear in the model
• tradeoff between fit and size of the coefs
• note familiarity with trees

ISLR simulation

A simulated data set containing \(p = 45\) predictors and \(n = 50\) observations.

ILSR 6.5 Squared bias (black), variance (green), and test mean squared error (purple) for the ridge regression predictions on a simulated data set, as a function of \(\lambda\) (left) and the standardize \(\ell_2\) norm (right). The horizontal dashed lines indicate the minimum possible MSE. The purple crosses indicate the models for which the MSE is smallest.

• \(\lambda < 10\) = 1e+01, the variance decreases rapidly, with very little increase in bias (hence MSE test drops considerably)
• \(\lambda\) = 0 = OLS, variance is high / bias low.

why right panel? - more comparable to the bias-trade off plots that we’re used to seeing. - From left to right: more flexible (bias decreases and the variance increases). - x-axis: coefficient estimates divided by the ℓ2 norm of the least squares estimates - these are the same pictures essentially but the y-axis on the RHS plotted against the $$2 norm of the ridge regression coefficient estimates divided by the $$2 norm of the least squares estimates.

Scaling of predictors

• Least squares coefficients are scale equivariant

  • i.e. multiplying \(X_j\) by a constant \(c\) leads to a scaling of the least squares coefficient estimates by a factor of \(1/c\).

• In contrast, the ridge regression coefficient estimates can change substantially when multiplying a given predictor by a constant

  • Why? since we use the sum of squared coefficients in the penalty term of the ridge regression objective function.

• If I multiply a feature by a constant it’s not going to matter because I can divide the coefficient by the same constant I get the same answer
• So it makes all the predictors comparable (and therefore their coefficients comperable)

Scaling of predictors (cont’d)

• Therefore, it is best to apply ridge regression after standardizing the predictors, using the formula

\[\begin{equation} \tilde{x}_{ij} = \frac{x_{ij}}{\frac{1}{n} \sum_{i=1}^n (x_{ij} - \overline{x}_j)^2} \end{equation}\]

• Software will peform centering and standardizing by default and reports answers back on original scale.

• denominator: the estimated standard deviation of the jth predictor
• all of the standardized predictors will have a standard deviation of one

Comment

• Unlike subset selection, which will generally select models that involve just a subset of the variables, ridge regression will include all predictors in the final model.
• In other words, \(\beta\) coefficients approach 0 but never are actually equal to zero.
• But adopting a small change on our penalty term, we will be able shrink coefficients exactly to zero (and hence perform feature selection) \(\dots\)

• RR is not able to perform feature selection

Lasso

• The least absolute shrinkage and selection operator or LASSO is arguably the most popular modern method applied to linear models.

• It is quite similar to ridge regression only now it minimizes \[\begin{align*} RSS + \lambda \sum_{j=1}^p |\beta_j| \end{align*}\]

Important advantage: it will force some coefficients to 0 (whereas RR will only force them “close” to 0)

• where \(\lambda\) is a tuning parameter.
• \(\beta_j^2\) is replaced with \(|\beta_j|\)
• so it is performing variable selection
• Tibshirani invented it.
  

L1 regularization

Another way that you might see this model being presented is using the L1 norm; in other words, the LASSO uses the \(\ell_1\) penalty:

\[ \begin{align} \lambda || \beta ||_1 &= \lambda\left( | \beta_1 | + | \beta_2 | + \ldots + | \beta_p | \right)\\ &= \lambda\sum_{i=1}^p | \beta_i | \end{align} \]

Hence this method is also referred to as L1 regularization.

LASSO Coefficients

Unlike least squares, ridge regression will produce a different set of coefficient estimates, \(\beta^R_\lambda\), for each value of \(\lambda\)

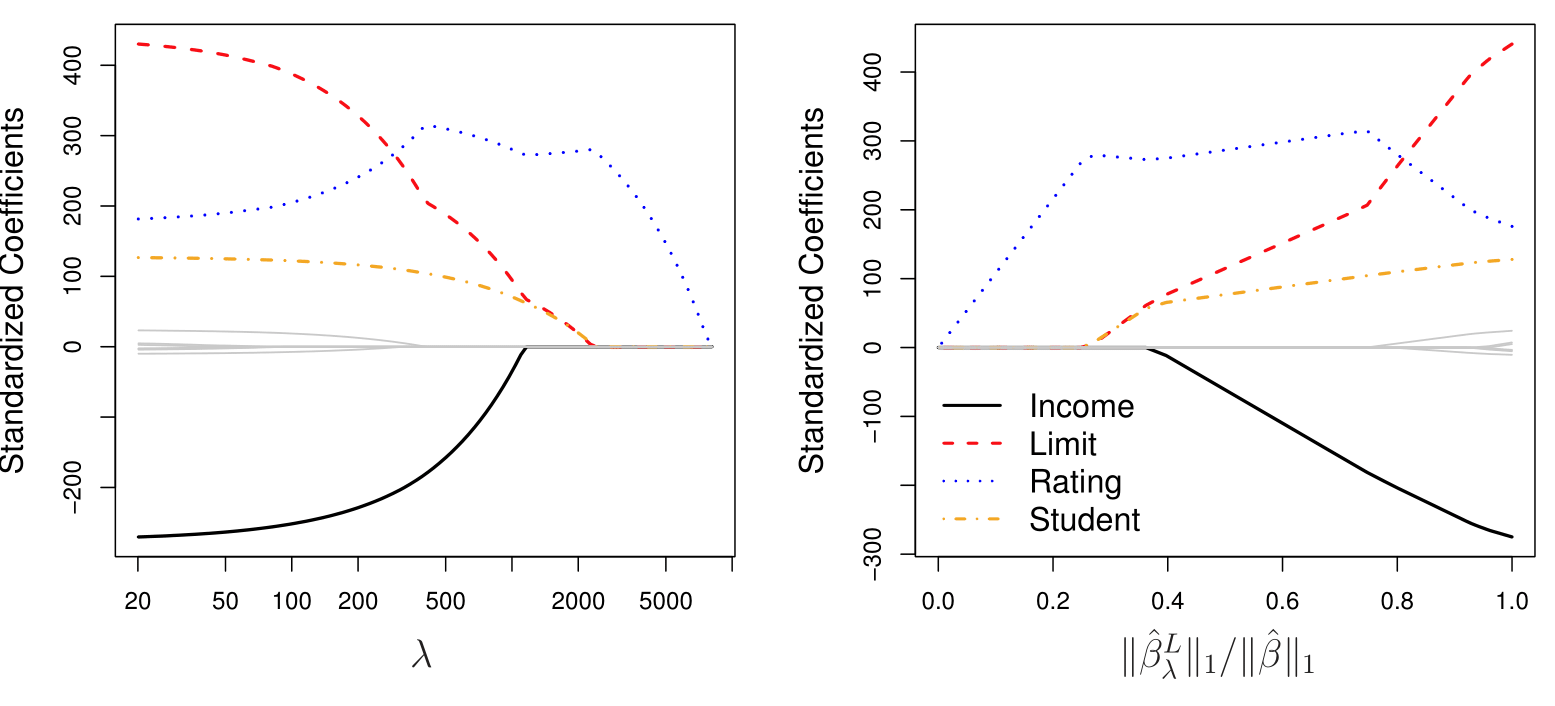
ILSR FIg 6.6: The standardized lasso coefficients on the Credit data set are shown as a function of \(\lambda\) and standardized \(\ell_2\) norm.

From left to right (in Right panel):

• 0 = null model (all 0 coefficients)
• first only rating
• then student and limit enter the model almost simultaneously,
• shortly followed by income.

Eventually, the remaining variables enter the model.

• Hence, depending on the value of λ, the lasso can produce a model involving any number of variables.
• In contrast, ridge regression will always include all of the variables in the model, although the magnitude of the coefficient estimates will depend on λ.

standardized coefficients (cuz we scaled)

Benefits of LASSO

• It is worth repeating that the \(\ell_1\) penalty forces some of the coefficient estimates to be exactly equal to zero when the tuning parameter \(\lambda\) is sufficiently large

• Hence the lasso performs variable selection

• As a result, models generated from the lasso are generally much easier to interpret than those of ridge regression

• We say that the lasso yields “sparse” models — that is, sparse models that involve only a subset of the variables.

Benefits of Ridge Regression

• The lasso implicitly assumes that a number of the coefficients truly equal zero

• When this is not the case, i.e. all predictors are useful, Ridge Regression would leads to better prediction accuracy

• These two examples illustrate that neither ridge regression nor the lasso will universally dominate the other.

• The choice between Ridge Regression and LASSO can also boil down to the Prediction vs. Inference trade off (aka Accuracy-Interpretability trade off);

When to use what?

• One might expect the lasso to perform better in a setting where a relatively small number of predictors have substantial coefficients, and the remaining predictors have coefficients that are very small or that equal zero

• Ridge regression will perform better when the response is a function of many predictors, all with coefficients of roughly equal size.

• Since we do not typically know this, a technique such as cross-validation can be used in order to determine which approach is better on a particular data set.

When to use Regularization

\(p > n\)

• These methods are most suitable when \(p > n\).

• Even when \(p < n\) these approaches (especially lasso) is popular with large data sets to fit a linear regression model and perform variable selection simultaneously.

• Being able to find, so-called “sparse” (as opposed to “dense”) models that select a small number of predictive variables in high-dimensional datasets is tremendously important/useful.

• variable selection is extremely important
• eg test for disease using 30K gene expressions (too expensive) so instead we find a test that works well on only 10 genes, that could be a major breakthrough
• much more meaningful for inference

When to use Regularization

Multicollinearity

• Less obviously, when you have multicollinearity¹ in your data, the least squares estimates have high variance.

• Furthermore, multicollinearity makes it difficult to distinguish which which variables (if any) are truly useful.

• Using the same argument as before, we can use ridge regression and lasso to reduce the variance and improve prediction accuracy and simultaneous shrink the coefficients of redundant predictors.

• by “useful” i mean predictive of the outcome.

• In the high-dimensional setting, the multicollinearity problem is a serious problem and makes it impossible to istinguish which which variables (if any) truly are predictive of the outcome

• At most, we can hope to assign large regression coefficients to variables that are correlated with the variables that truly are predictive of the outcome.

1. when two or more predictors in a regression are correlated with each other

Multicollinearity in Credit

pairs(Credit[,1:3])

• We can see that multicollinearity is an issue for the credit data for example.

• credit limit is highly related to credit rating

• and both or those are possitively correlated with income for example

Choosing \(\lambda\)

• Both the lasso and ridge regression require specification of \(\lambda\)

• In fact, for each value of \(\lambda\) we will see different coefficients.

• So how do we find the best one?

• The answer, as you may have guessed, is cross-validation.

similar to the \(\lambda\) parameter from our penalized MSE for pruning back trees

glmnet

To perform regression with regularization we use the function glmnet function (from package glmnet )

glmnet(x, y, ... )

• Note that glmnet does not allow the formula argument.

• Hence we will need specify x and y.

N.B. there is a handy helper function model.matrix() that will help us do this.

• pronounced “glim - net”

glmnet penalty

glmnet(x, y, alpha = 1, ... )

The penalty used is: \[ \frac{(1-\alpha)}{2} || \beta ||_2^2 + \alpha ||\beta||_1 \]

• alpha=1 is the lasso penalty \(||\beta||_1\) (default)

• alpha=0 is the ridge penalty

Values between 0 and 1 are allowed and correspond to elasticnet (this model is not discuss here or in the book).

glmnet \(\lambda\)

glmnet(x, y, alpha = 1, nlambda = 100 ... )

• A grid of values for the regularization parameter \(\lambda\) is considered

• nlambda is the number of \(\lambda\) values considered in the grid (the default is 100)

• The actually values are determined by nlambda and lambda.min.ratio (see the help file for more on this)

• Alternatively, the user may supply a sequence for \(\lambda\) (in the optional lambda argument), but this is not recommended.

glmnet standardizing and family

glmnet(x, y, alpha = 1, nlambda = 100, standardize = TRUE,
  family = c("gaussian", "binomial", "poisson", "multinomial", "cox", "mgaussian"), ... )

By default the function standardizes the data¹

While we talked about these concepts in the context of linear regression, they can be extended to logistic and multinomial, and poisson regression

1. Coefficient estimates then transformed back onto original scale (by multiply back up by standard deviation) for the results.

Cross-validation

• In order to determine the best choice for \(\lambda\) we use cross-validation

• The cv.glmnet function from the same package will perform \(k\)-fold cross-validation for glmnet (default is 10-fold)

• From that we produce a plot that returns good value(s) for \(\lambda\).

helper function

library(glmnet); library(ISLR2); data(Credit)
x <- model.matrix(Balance~., Credit)[,-1]
y <- Credit$Balance

The model.matrix() function is particularly useful for creating x; not only does it produce a matrix corresponding to the predictors but it also automatically transforms any qualitative variables into dummy variables¹

• model.matrix is borrowed form the stats package
• [,-1] is to say we don’t need the intercept column (the intercept will still be fit but that is controlled within the function: glmnet(x, y, alpha = 1, intercept = FALSE))
• model.matrix(Balance~.-1, Credit) should do the same but some reason when you code it like that TWO dummy variables gets made for Own (yes/no)

1. this is important since glmnet() can only take numerical, quantitative inputs

Lasso with Credit

lasso <-  glmnet(x = x, y = y, family = "gaussian", alpha = 1)
plot(lasso, xvar = "lambda")

• Options for xvar are “norm”, “lambda”, “dev” (default is L1 norm)
• label = TRUE to label the curves
• ?plot.glmnet for details

Lasso Coefficient Estimates

To see the values for the coefficient estimates use coef(). For example to the see coefficients produced when \(\lambda\) the 60th value in our sequence ( log \(\lambda\) = 0.4938434 in this case):

coef(lasso)[,60]

 (Intercept)       Income        Limit       Rating        Cards          Age 
-483.4397780   -7.5851123    0.1704558    1.3900860   15.4997658   -0.5597635 
   Education       OwnYes   StudentYes   MarriedYes  RegionSouth   RegionWest 
  -0.5160200   -6.8245847  418.6128482   -5.3459725    2.1876891    7.6654500 

Ridge Regression with Credit

Cross-validation for RR

set.seed(10) # use cross-validation to choose the tuning parameter
cv.out.rr <- cv.glmnet(x, y, alpha = 0)
plot(cv.out.rr);  log(bestlam <- cv.out.rr$lambda.min)

[1] 3.680249

• the first (left-most) vertical dotted line is the best lambda (min)
• the second vertical dotted line is a second choice (the largest lambda that is within 1 standard error of the minimum)
• the second is a more restricted model that does almost as well (maybe even better) as the minimum
• 11 = at all stages we have all 11 predictors in our model

Cross-validation for Lasso

set.seed(1) # use cross-validation to choose the tuning parameter
cv.out.lasso <- cv.glmnet(x, y, alpha = 1)
plot(cv.out.lasso);  log(bestlam <- cv.out.lasso$lambda.min)

[1] -0.5295277

• similar plot for lasso.
  
• note the number of variables (11 - 6 = 5)

CV output plot

The cv.glmnet ouptut plot produced from a simulation that you will see in lab

Beer

beer.lm = lm(price~., data=beer[,-1]); summary(beer.lm)

...

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.7174521  0.6807382   5.461 8.56e-07 ***
qlty        -0.0111435  0.0064446  -1.729   0.0887 .  
cal         -0.0055034  0.0089957  -0.612   0.5429    
alc          0.0764520  0.1752318   0.436   0.6641    
bitter       0.0677117  0.0153219   4.419 3.98e-05 ***
malty        0.0002832  0.0099639   0.028   0.9774    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.8661 on 63 degrees of freedom
Multiple R-squared:  0.6678,    Adjusted R-squared:  0.6415 
F-statistic: 25.33 on 5 and 63 DF,  p-value: 6.588e-14
...

Lasso on beer

lasso <-  glmnet( x = beer[,c(3:7)], y = beer[,2], family = "gaussian", alpha = 1)
plot(lasso, xvar = "lambda")

Best \(\lambda\) for LASSO

Lasso on beer

# superimpose the best lambda on trace plot
plot(lasso, xvar = "lambda")
abline(v = log(bestlam.lasso), col = "gray", lwd = 2, lty = 2)

Lasso on beer

library(plotmo) # allows us to label the x biggest coefs
plot_glmnet(lasso, xvar = "lambda", label = 5)
abline(v = log(bestlam.lasso), col = "gray", lwd = 2, lty = 2)

Lasso on beer

library(plotmo) # allows us to label the x biggest coefs
plot_glmnet(lasso, xvar = "lambda", label = 5)
lambda2 = cv.out.lasso$lambda.1se # 2nd choice 
abline(v = log(lambda2), col = "gray", lwd = 2, lty = 2)

Coefficients

cbind(coef(beer.lm),  # OLS (least squares estimates)
      # LASSO estimates ...
      coef(lasso, s = bestlam.lasso), # ... at best lambda
      coef(lasso, s = lambda2))       # ... at lambba within 1 s.e.

6 x 3 sparse Matrix of class "dgCMatrix"
                                    s1         s1
(Intercept)  3.7174521392  3.334440257 3.25063467
qlty        -0.0111434572 -0.008782345 .         
cal         -0.0055034319  .           .         
alc          0.0764519623  .           .         
bitter       0.0677117274  0.062008057 0.04831986
malty        0.0002831604  .           .         

Summary

• Ridge regression and LASSO works best in situations where the least squares estimates have high variance.

  • This can happen when \(p\) exceeds (or is close to \(n\))

  • It can also happen when we have multicollinearity

• LASSO shrinks coefficient estimates to exactly 0 hence it can be viewed as a variable selection technique

• Ridge Regression shrinks coefficient estimates close to 0 so it never actually eliminates any predictors.

Different Formulation

The coefficient estimates can be reformulated to solving the following two problems.

Lasso regression solve:

\[ \text{minimize} \quad \sum_{i=1}^{n} \left(y_i - \beta_0 - \sum_{j=1}^{p} \beta_j x_{ij}\right)^2 \quad \text{subject to} \quad \sum_{j=1}^{p} |\beta_j| \leq s \]

Ridge regression solves:

\[ \text{minimize} \quad \sum_{i=1}^{n} \left(y_i - \beta_0 - \sum_{j=1}^{p} \beta_j x_{ij}\right)^2 \quad \text{subject to} \quad \sum_{j=1}^{p} \beta_j^2 \leq s \]

• For every value of λ, there is some \(s\) such that the Equations RSS+λ\(\Sigma\)|βj| and (1) will give the same lasso coefficient estimate
• we’re trying to find the set of coefficient estimates that lead to the smallest RSS, subject to the constraint \(|\beta_j| \leq s\) (our budget)

Contours of the error and constraint functions for the lasso (left) and ridge regression (right). The solid blue areas are the constraint regions, \(|\beta_1| + |\beta_2| \leq s\) and \(\beta_1^2 + \beta_2^2 \leq s\), while the red ellipses are the contours of the RSS.

• OLS = \(\hat \beta\)
• Each of the ellipses centered around \(\hat \beta\) represents a contour: this means that all of the points on a particular ellipse have the same RSS value
• As the ellipses expand away from the least squares coefficient estimates, the RSS increases.
• circle = RR constraint
• diamond = LASSO constraint
• \(s\) makes those shapes bigger/smaller
• If \(s\) is sufficiently large, then the constraint regions will contain \(\hat \beta\), and the RR/LASSO estimates == OLS estimates
• When \(s\) gets smaller, the shapes get smaller at \(\hat \beta\) falls outside of diamond and circle (constraint region)
• The equations indicate that the RR/LASSO coefficient estimates are given by the first point at which an ellipse contacts the constraint region (circle/diamond).
• Since ridge regression has a circular constraint with no sharp points, this intersection will not generally occur on an axis, and so the ridge regression coefficient estimates will be exclusively non-zero.
• However, the lasso constraint has corners at each of the axes, and so the ellipse will often intersect the constraint region at an axis.
• In Figure 6.7, the intersection occurs at β1 = 0, and so the resulting model will only include β2.